View Jupyter notebook on the GitHub.
Forecasting interpretation#
This notebook contains examples of forecast decomposition into additive components for various models.
Table of contents
Loading dataset
Forecast decomposition
CatBoost
SARIMAX
BATS
In-sample and out-of-sample decomposition
Accessing target components
Regressors relevance
Feature relevance
Components relevance
[1]:
import warnings
warnings.filterwarnings("ignore")
[2]:
from copy import deepcopy
import pandas as pd
from etna.analysis import plot_backtest
from etna.analysis import plot_forecast_decomposition
from etna.datasets import TSDataset
from etna.metrics import MAE
from etna.pipeline import Pipeline
from etna.transforms import LagTransform
[3]:
HORIZON = 21
1. Loading dataset#
Consider the dataset data/example_dataset.csv.
We will use this data to demonstrate how model forecasts can be decomposed down to additive effects in the ETNA library.
Let’s load and plot this data to get a brief idea of how time series look.
[4]:
df = pd.read_csv("data/example_dataset.csv")
df["timestamp"] = pd.to_datetime(df["timestamp"])
ts = TSDataset(df, freq="D")
ts.head(5)
[4]:
| segment | segment_a | segment_b | segment_c | segment_d |
|---|---|---|---|---|
| feature | target | target | target | target |
| timestamp | ||||
| 2019-01-01 | 170 | 102 | 92 | 238 |
| 2019-01-02 | 243 | 123 | 107 | 358 |
| 2019-01-03 | 267 | 130 | 103 | 366 |
| 2019-01-04 | 287 | 138 | 103 | 385 |
| 2019-01-05 | 279 | 137 | 104 | 384 |
[5]:
ts.plot()
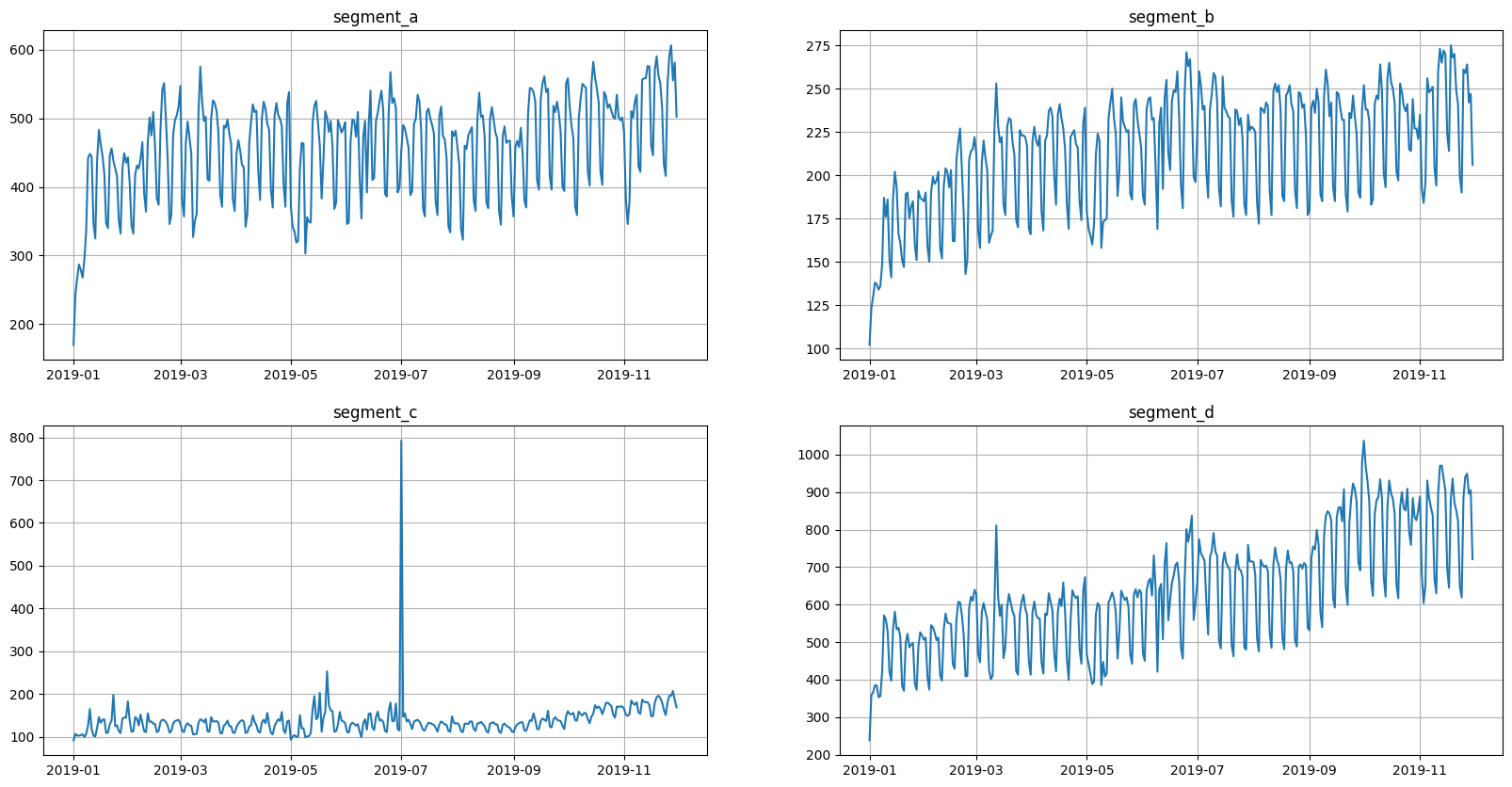
Here we have four segments in the dataset. All segments have seasonalities, and some of them show signs of trend.
Some of the models need features in order to estimate forecasts. Here we will use lags of the target variable as features when it is necessary.
[6]:
transforms = [
LagTransform(in_column="target", lags=list(range(21, 57, 7)), out_column="lag"),
]
2. Forecast decomposition#
This section shows how a model forecast can be decomposed down to individual additive components. There are two types of decomposition:
model-specific decomposition
model-agnostic decomposition
Model-specific decomposition uses model representation to compute components. Consider linear regression as an example. \(\hat y = w^T X + b\). We can slightly rewrite this equation to see additive components \(\hat y = \sum_{i=0}^m w_i x_i + b\). So in this case, the components are: \(w_i x_i\) and \(b\).
Model-agnostic decomposition uses separate estimators to compute the contribution of each component (e.g., SHAP).
The main feature of forecast decomposition in the ETNA library is guaranteed additive components.
There are several models with available decomposition:
SARIMAXModelAutoARIMAModelCatBoostPerSegmentModel,CatBoostMultiSegmentModelSimpleExpSmoothingModel,HoltModel,HoltWintersModelLinearPerSegmentModel,ElasticPerSegmentModel,LinearMultiSegmentModel,ElasticMultiSegmentModelProphetModelMovingAverageModel,NaiveModel,DeadlineMovingAverageModel,SeasonalMovingAverageModelBATS,TBATS
In this notebook, we will take a closer look at the forecast decomposition for CatBoost, SARIMAX and BATS.
Here is a function that will help us extract the target and its components from the forecast dataframe and transform this data to TSDataset.
[7]:
from etna.datasets.utils import match_target_components
def target_components_to_ts(df: pd.DataFrame) -> TSDataset:
"""Get components with target as `TSDataset`."""
# find target components column names
column_names = set(df.columns.get_level_values("feature"))
components_columns = match_target_components(column_names)
# select dataframe with components
target_components = df.loc[:, pd.IndexSlice[:, tuple(components_columns)]]
# select dataframe with target
target = df.loc[:, pd.IndexSlice[:, "target"]]
# creat dataset
forecast_ts = TSDataset(df=target, freq="D")
forecast_ts.add_target_components(target_components_df=target_components)
return forecast_ts
2.1 CatBoost#
CatBoost uses model-agnostic forecast decomposition. Components contributions estimated with SHAP for each timestamp. Decomposition at timestamp \(t\) could be represented as:
\begin{equation} f(x_t) = \phi_0 + \sum_{i = 1}^m \phi_i \quad , \end{equation}
where \(\phi_i\) - SHAP values.
[8]:
from etna.models import CatBoostMultiSegmentModel
from etna.models import CatBoostPerSegmentModel
Here we create Pipeline with CatBoostPerSegmentModel and estimate forecast components.
[9]:
pipeline = Pipeline(model=CatBoostPerSegmentModel(), transforms=transforms, horizon=HORIZON)
_, forecast_df, _ = pipeline.backtest(ts=ts, metrics=[MAE()], n_folds=3, forecast_params={"return_components": True})
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 1.8s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 3.6s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 5.5s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 5.5s
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.3s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.6s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 1.0s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 1.0s
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.0s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.0s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.1s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.1s
[10]:
plot_backtest(forecast_df=forecast_df, ts=ts, history_len=50)
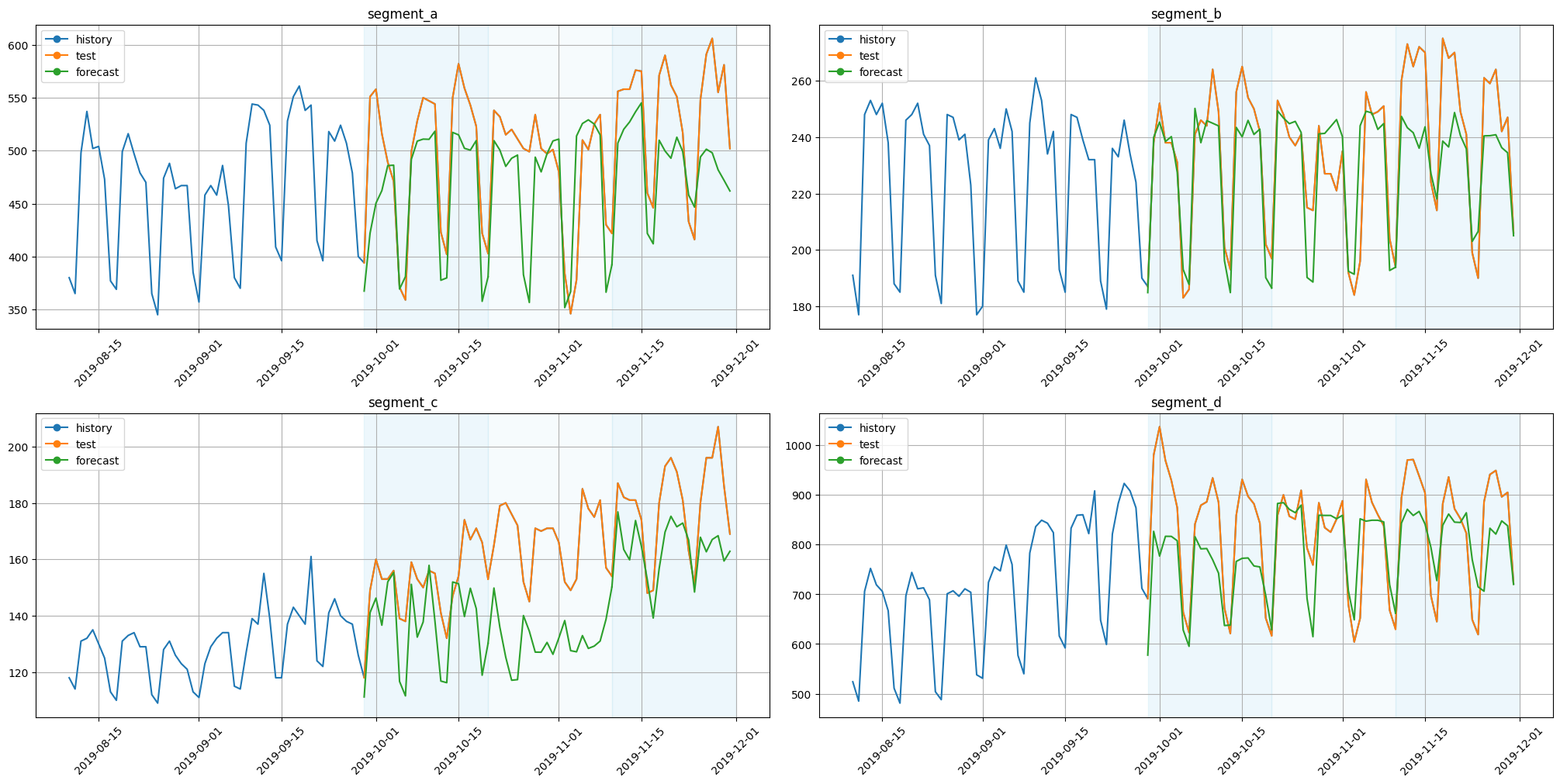
Components could be plotted with the function plot_forecast_decomposition.
[11]:
forecast_ts = target_components_to_ts(df=forecast_df)
plot_forecast_decomposition(forecast_ts=forecast_ts, mode="joint", columns_num=2, show_grid=True)
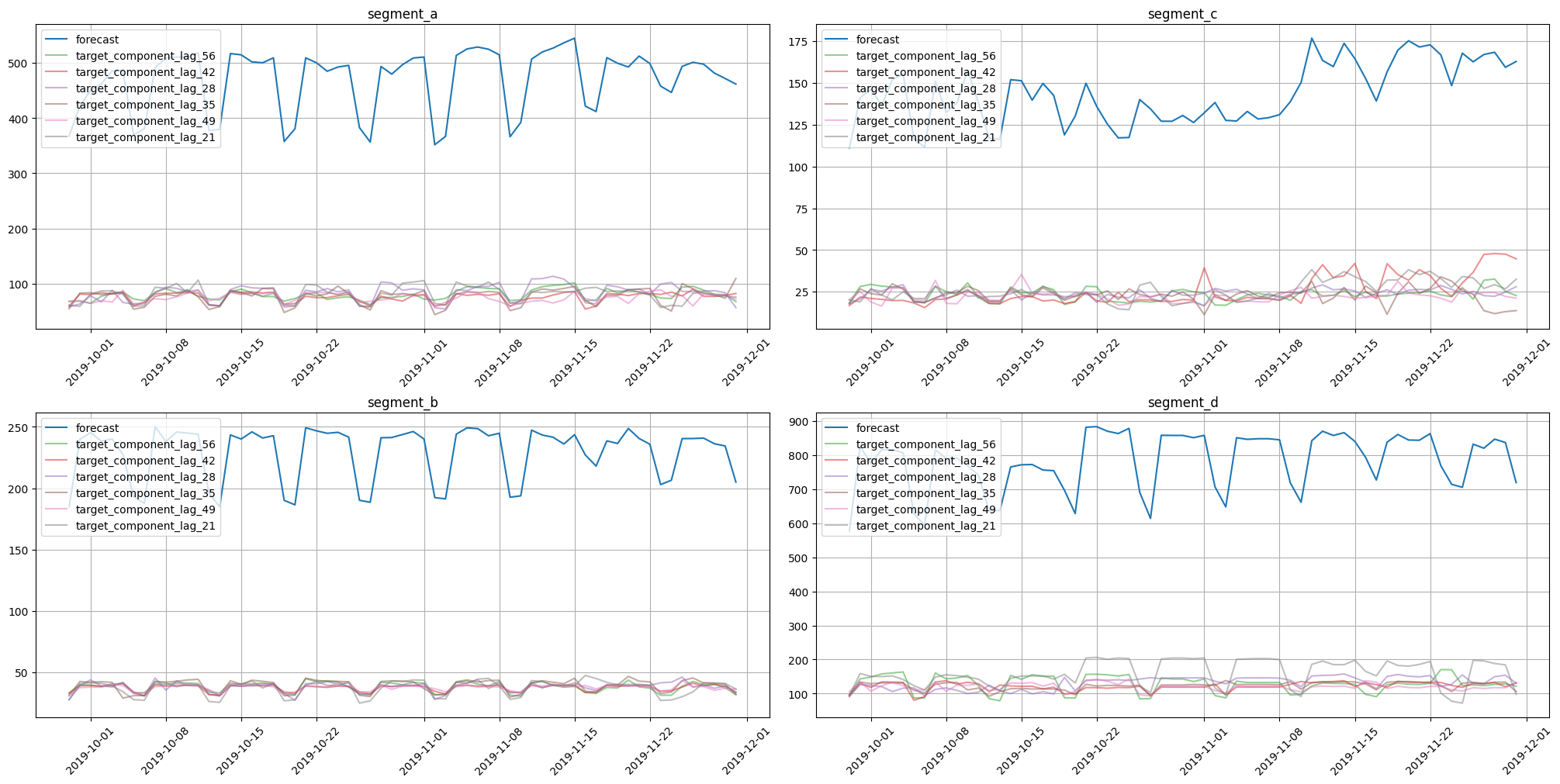
On these charts we can see how each feature contributed to the forecast for each timestamp. CatBoost uses features to estimate forecasts, so each forecast component corresponds to a particular feature.
Let’s run a similar procedure for CatBoostMultiSegmentModel.
[12]:
pipeline = Pipeline(model=CatBoostMultiSegmentModel(), transforms=transforms, horizon=HORIZON)
_, forecast_df, _ = pipeline.backtest(ts=ts, metrics=[MAE()], n_folds=3, forecast_params={"return_components": True})
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 1.2s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 2.3s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 3.6s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 3.6s
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.3s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.7s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 1.0s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 1.0s
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.0s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.1s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.1s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.1s
[13]:
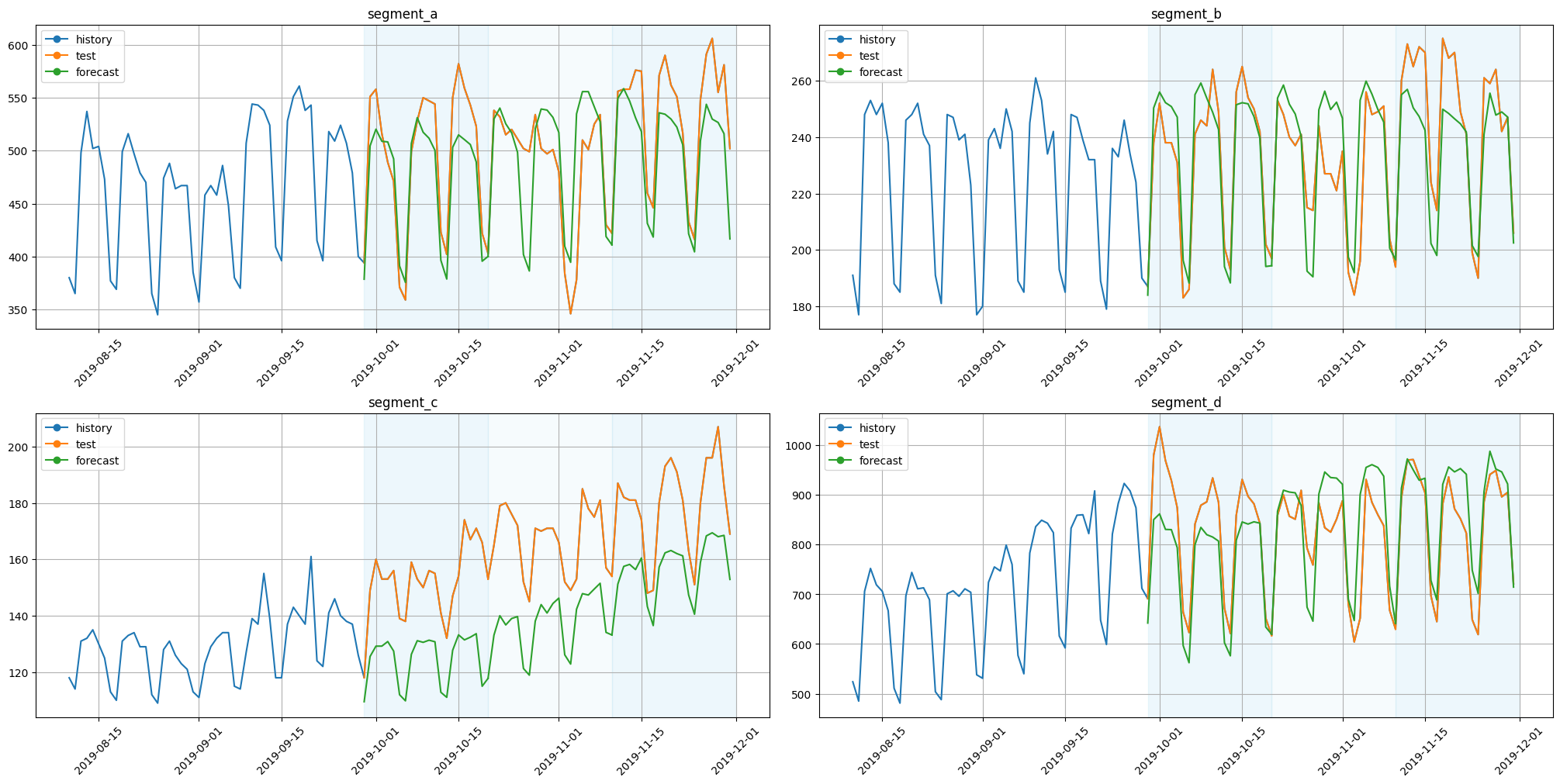
plot_backtest(forecast_df=forecast_df, ts=ts, history_len=50)
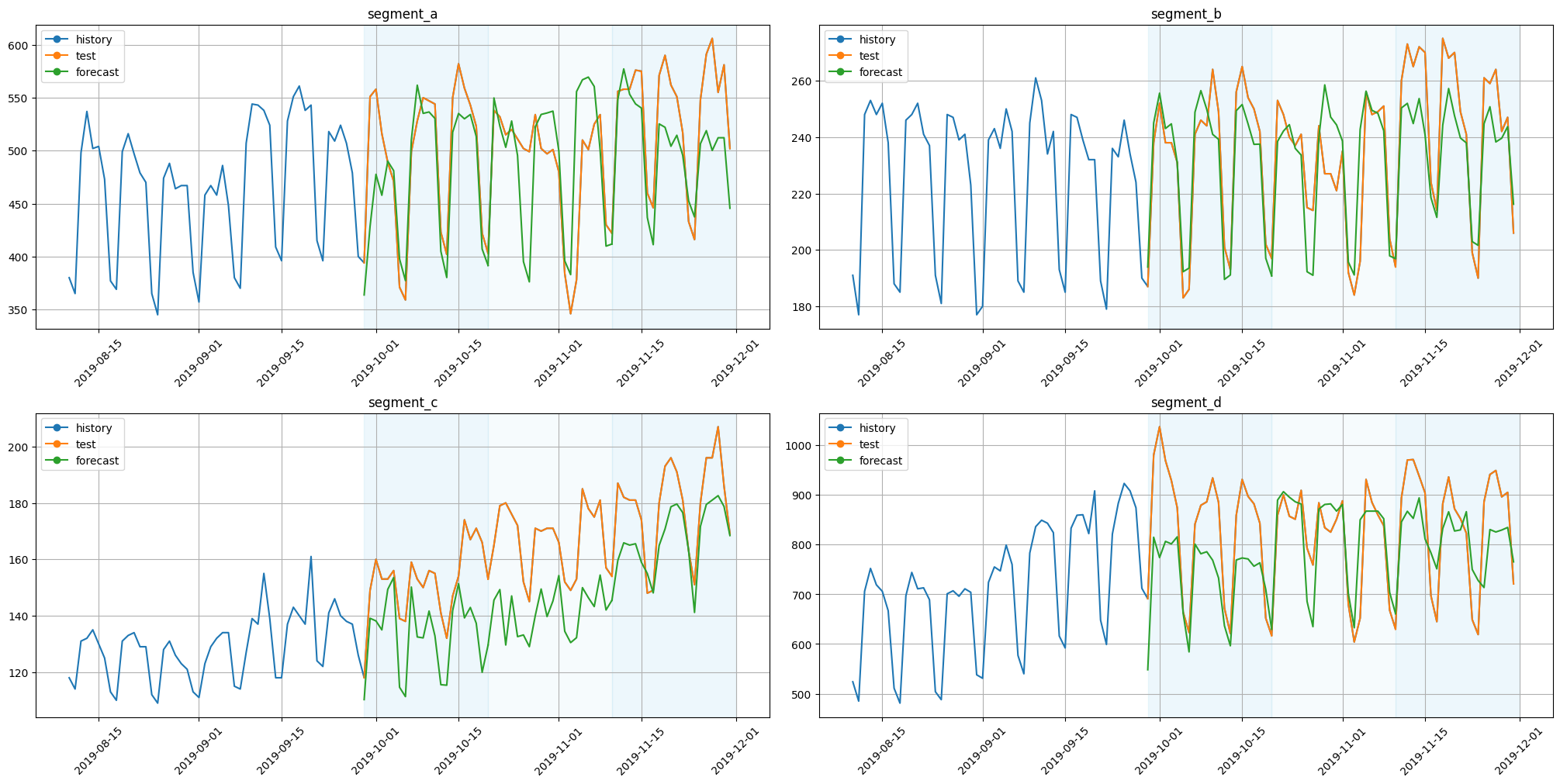
[14]:
forecast_ts = target_components_to_ts(df=forecast_df)
plot_forecast_decomposition(forecast_ts=forecast_ts, mode="joint", columns_num=2, show_grid=True)
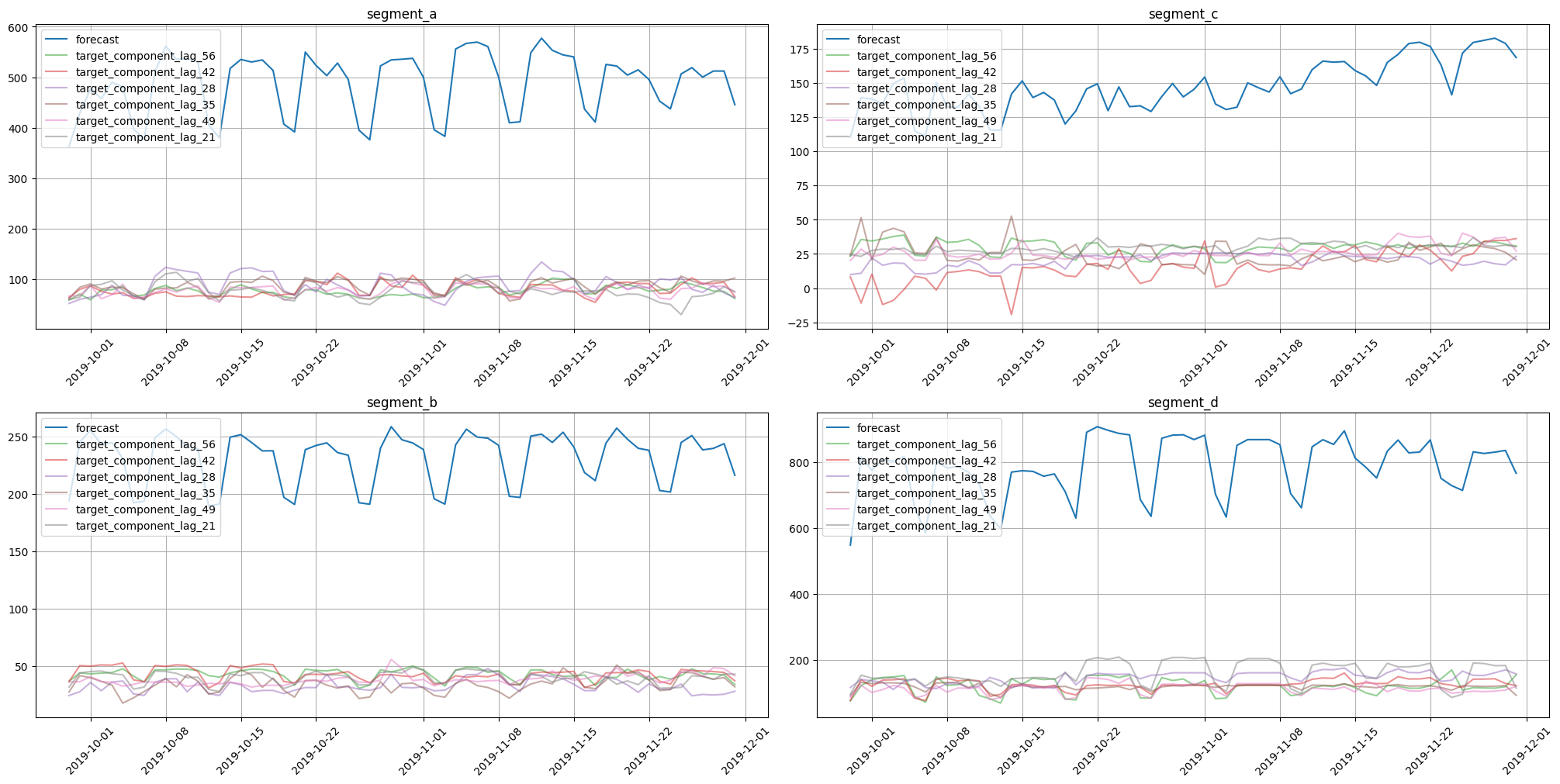
Here we obtained almost similar results. They are identical in structure but slightly different when comparing values. Such behaviour is explained by the use of a single model for all dataset segments.
2.2 SARIMAX#
SARIMAX uses model-specific forecast decomposition. So the main components of this model are: SARIMA and effects from exogenous variables.
Such constraints on decomposition form are due to implementation details of SARIMAX models, which are estimated as state-space models.
[15]:
from etna.models import SARIMAXModel
Let’s build Pipeline with SARIMAXModel and estimate forecast components on backtest.
[16]:
pipeline = Pipeline(model=SARIMAXModel(), transforms=transforms, horizon=HORIZON)
_, forecast_df, _ = pipeline.backtest(ts=ts, metrics=[MAE()], n_folds=3, forecast_params={"return_components": True})
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 4.90038D+00 |proj g|= 1.65569D-01
At iterate 5 f= 4.85680D+00 |proj g|= 2.10363D-02
At iterate 10 f= 4.85558D+00 |proj g|= 4.19482D-03
At iterate 15 f= 4.85420D+00 |proj g|= 2.79606D-02
At iterate 20 f= 4.85376D+00 |proj g|= 7.24822D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 22 27 1 0 0 1.529D-05 4.854D+00
F = 4.8537570835596506
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 4.00764D+00 |proj g|= 2.03374D-01
At iterate 5 f= 3.97187D+00 |proj g|= 9.69939D-03
At iterate 10 f= 3.97079D+00 |proj g|= 7.25716D-03
At iterate 15 f= 3.97049D+00 |proj g|= 7.69284D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 18 24 1 0 0 1.597D-05 3.970D+00
F = 3.9704937260313664
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
This problem is unconstrained.
This problem is unconstrained.
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 5.34706D+00 |proj g|= 1.90556D-02
At iterate 5 f= 5.34701D+00 |proj g|= 8.87463D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 5 8 1 0 0 8.875D-05 5.347D+00
F = 5.3470110236236659
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 5.41327D+00 |proj g|= 2.29720D-01
At iterate 5 f= 5.37417D+00 |proj g|= 1.87453D-02
At iterate 10 f= 5.37332D+00 |proj g|= 3.59795D-03
At iterate 15 f= 5.37261D+00 |proj g|= 2.76053D-02
At iterate 20 f= 5.37180D+00 |proj g|= 4.27622D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 22 26 1 0 0 1.226D-05 5.372D+00
F = 5.3718041615424870
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 4.87110D+00 |proj g|= 1.54798D-01
This problem is unconstrained.
This problem is unconstrained.
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.4s
This problem is unconstrained.
At iterate 5 f= 4.82551D+00 |proj g|= 4.04983D-02
At iterate 10 f= 4.82384D+00 |proj g|= 3.86702D-03
At iterate 15 f= 4.82355D+00 |proj g|= 1.76847D-02
At iterate 20 f= 4.82168D+00 |proj g|= 5.25136D-03
At iterate 25 f= 4.82166D+00 |proj g|= 1.07272D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 25 31 1 0 0 1.073D-04 4.822D+00
F = 4.8216622881090307
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 3.97752D+00 |proj g|= 2.10289D-01
At iterate 5 f= 3.94348D+00 |proj g|= 8.76676D-03
At iterate 10 f= 3.94254D+00 |proj g|= 1.20056D-02
At iterate 15 f= 3.94231D+00 |proj g|= 2.84316D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 17 23 1 0 0 1.044D-05 3.942D+00
F = 3.9423131829987743
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
This problem is unconstrained.
This problem is unconstrained.
This problem is unconstrained.
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 5.31323D+00 |proj g|= 2.61433D-02
At iterate 5 f= 5.31314D+00 |proj g|= 8.69485D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 5 8 1 0 0 8.695D-05 5.313D+00
F = 5.3131410159230246
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 5.41440D+00 |proj g|= 3.15861D-01
At iterate 5 f= 5.35194D+00 |proj g|= 1.73456D-02
At iterate 10 f= 5.35100D+00 |proj g|= 3.07897D-03
At iterate 15 f= 5.34849D+00 |proj g|= 4.01631D-02
At iterate 20 f= 5.34688D+00 |proj g|= 9.88039D-04
At iterate 25 f= 5.34687D+00 |proj g|= 4.49029D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 26 31 1 0 0 3.804D-05 5.347D+00
F = 5.3468739885960970
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.8s
This problem is unconstrained.
This problem is unconstrained.
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 4.90986D+00 |proj g|= 2.31991D-01
At iterate 5 f= 4.86531D+00 |proj g|= 1.31344D-02
At iterate 10 f= 4.86491D+00 |proj g|= 1.14106D-02
At iterate 15 f= 4.86340D+00 |proj g|= 3.90127D-02
At iterate 20 f= 4.86307D+00 |proj g|= 2.96271D-03
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 23 28 1 0 0 5.929D-05 4.863D+00
F = 4.8630726840600804
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 4.00550D+00 |proj g|= 2.45513D-01
At iterate 5 f= 3.97878D+00 |proj g|= 5.34959D-03
At iterate 10 f= 3.97831D+00 |proj g|= 1.04488D-02
At iterate 15 f= 3.97818D+00 |proj g|= 2.67016D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 17 23 1 0 0 8.812D-06 3.978D+00
F = 3.9781845691380524
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 5.28379D+00 |proj g|= 3.50254D-02
At iterate 5 f= 5.28362D+00 |proj g|= 8.71784D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 5 8 1 0 0 8.718D-05 5.284D+00
F = 5.2836224381312107
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 8 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 5.44469D+00 |proj g|= 3.22756D-01
At iterate 5 f= 5.39435D+00 |proj g|= 1.21107D-02
At iterate 10 f= 5.39418D+00 |proj g|= 5.90180D-03
At iterate 15 f= 5.39219D+00 |proj g|= 5.58459D-02
At iterate 20 f= 5.39176D+00 |proj g|= 7.63151D-04
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
8 23 28 1 0 0 5.592D-05 5.392D+00
F = 5.3917592312532499
CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
This problem is unconstrained.
This problem is unconstrained.
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 1.3s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 1.3s
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.4s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.8s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 1.2s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 1.2s
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.0s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.0s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.1s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.1s
[17]:
plot_backtest(forecast_df=forecast_df, ts=ts, history_len=50)
[18]:
forecast_ts = target_components_to_ts(df=forecast_df)
plot_forecast_decomposition(forecast_ts=forecast_ts, mode="joint", columns_num=2, show_grid=True)
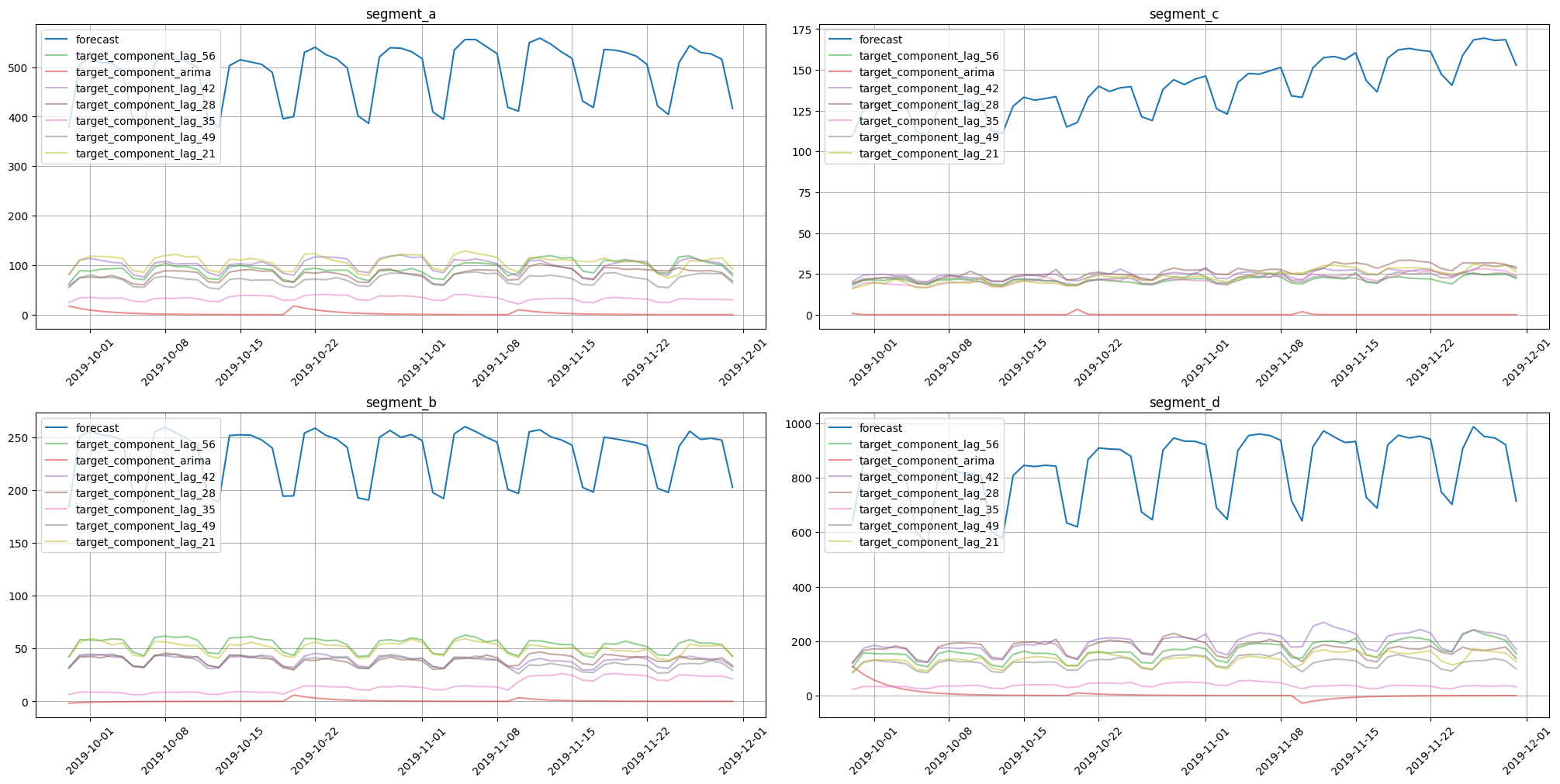
Here we can notice components for each exogenous variable and a separate component for the SARIMA effect. Note that this decomposition is completely different from the forecast decomposition of CatBoost models, even on the same data. This is due to different approaches for component contribution estimation.
2.3 BATS#
BATS uses model-specific forecast decomposition. The main components are:
trend
local level
seasonality for each specified period
errors ARMA(p, q)
The last two components are controlled by seasonal_periods and use_arma_erros parameters, respectively. The trend component is controlled by use_trend. These parameters add flexibility to the model representation and, hence, to the forecast decomposition.
[19]:
from etna.models import BATSModel
Let’s build Pipeline and estimate forecast decomposition with BATSModel, but now without any features.
[20]:
pipeline = Pipeline(model=BATSModel(seasonal_periods=[14, 21]), horizon=HORIZON)
_, forecast_df, _ = pipeline.backtest(ts=ts, metrics=[MAE()], n_folds=3, forecast_params={"return_components": True})
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 3.0min
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 6.5min
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 9.8min
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 9.8min
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.1s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.2s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.4s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.4s
[Parallel(n_jobs=1)]: Done 1 tasks | elapsed: 0.0s
[Parallel(n_jobs=1)]: Done 2 tasks | elapsed: 0.1s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.1s
[Parallel(n_jobs=1)]: Done 3 tasks | elapsed: 0.1s
[21]:
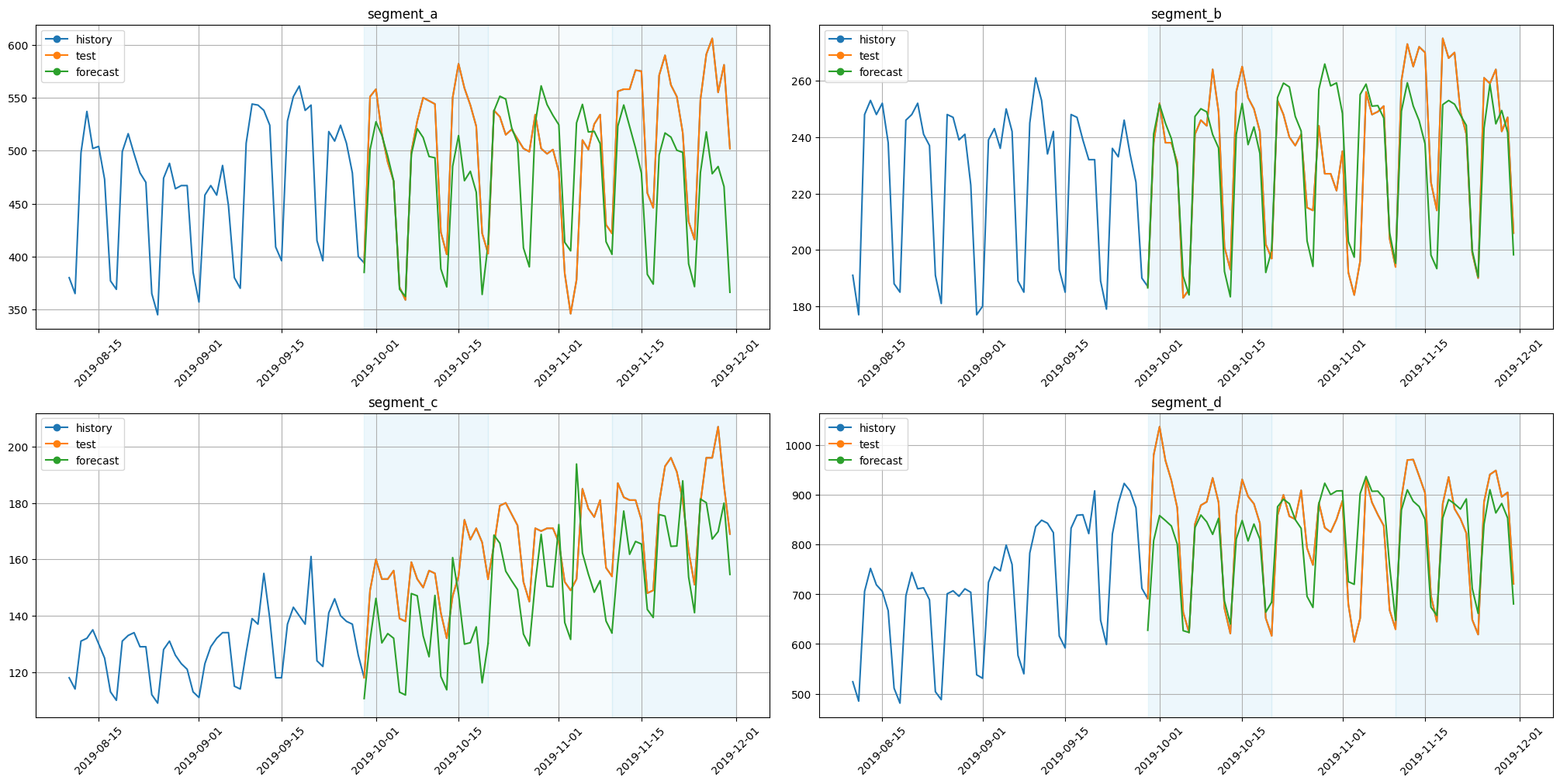
plot_backtest(forecast_df=forecast_df, ts=ts, history_len=50)
[22]:
forecast_ts = target_components_to_ts(df=forecast_df)
plot_forecast_decomposition(forecast_ts=forecast_ts, mode="joint", columns_num=2, show_grid=True)
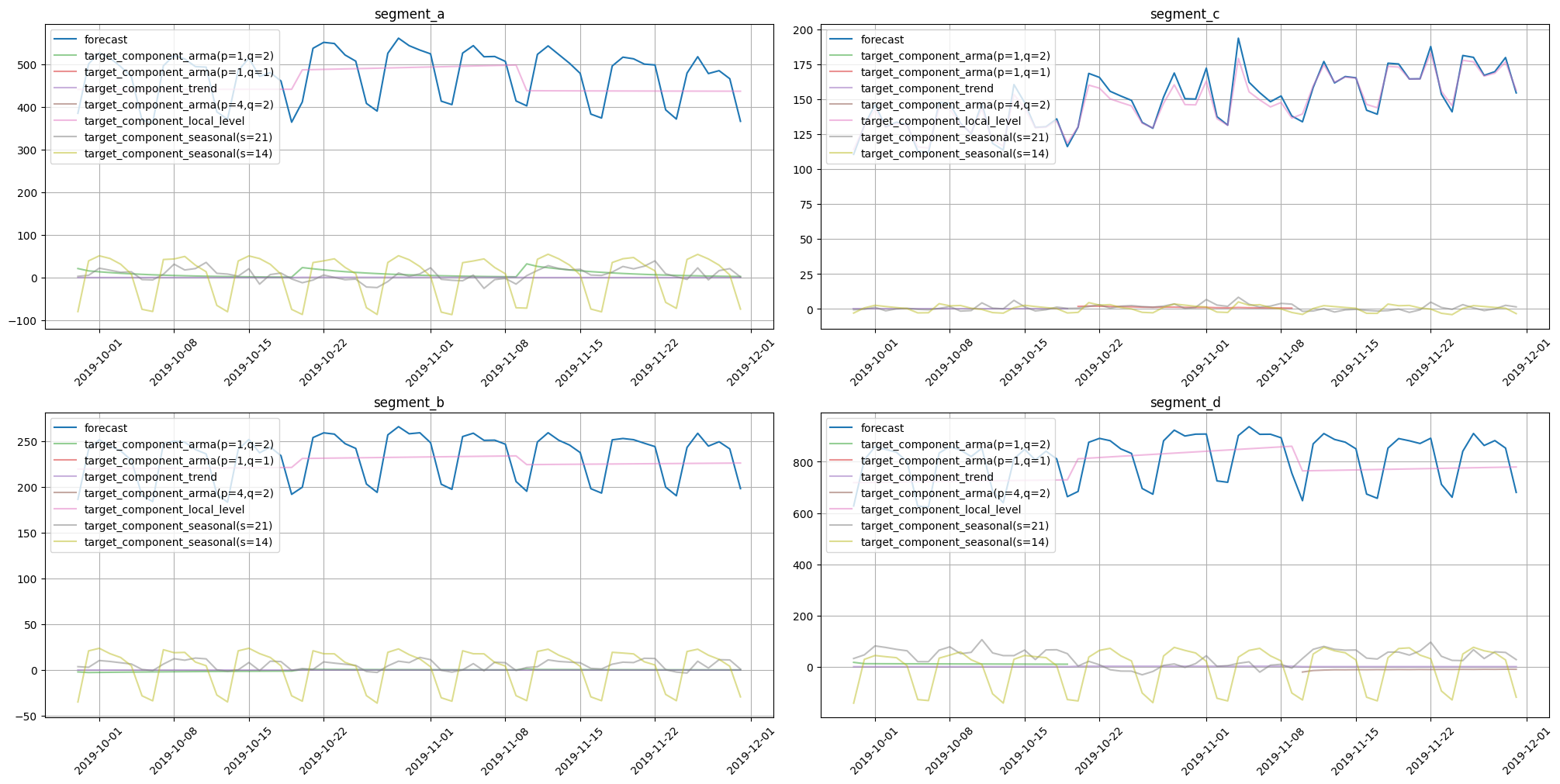
Here we obtained components for trend, local level, seasonality, and ARMA errors. Note that each seasonality period is represented by a separate component. Such a form of decomposition helps to find causality with seasonal effects in the original data. Results show that almost all seasonal fluctuations come from seasonality in period 14.
2.4 In-sample and out-of-sample decomposition#
In the ETNA library we can perform decomposition of fitted and forecasted values separately.
Consider the BATS model with seasonal periods of 2 and 3 weeks. Let’s prepare data for training and forecasting and fit the model.
[23]:
train, _ = ts.train_test_split(test_size=HORIZON)
future = train.make_future(future_steps=HORIZON)
model = BATSModel(seasonal_periods=[14, 21])
model.fit(ts=train);
In-sample forecast decomposition could be estimated with predict method. To do this set return_components=True.
[24]:
in_sample_forecast = model.predict(ts=train, return_components=True)
plot_forecast_decomposition(forecast_ts=in_sample_forecast, mode="joint", columns_num=2, show_grid=True)
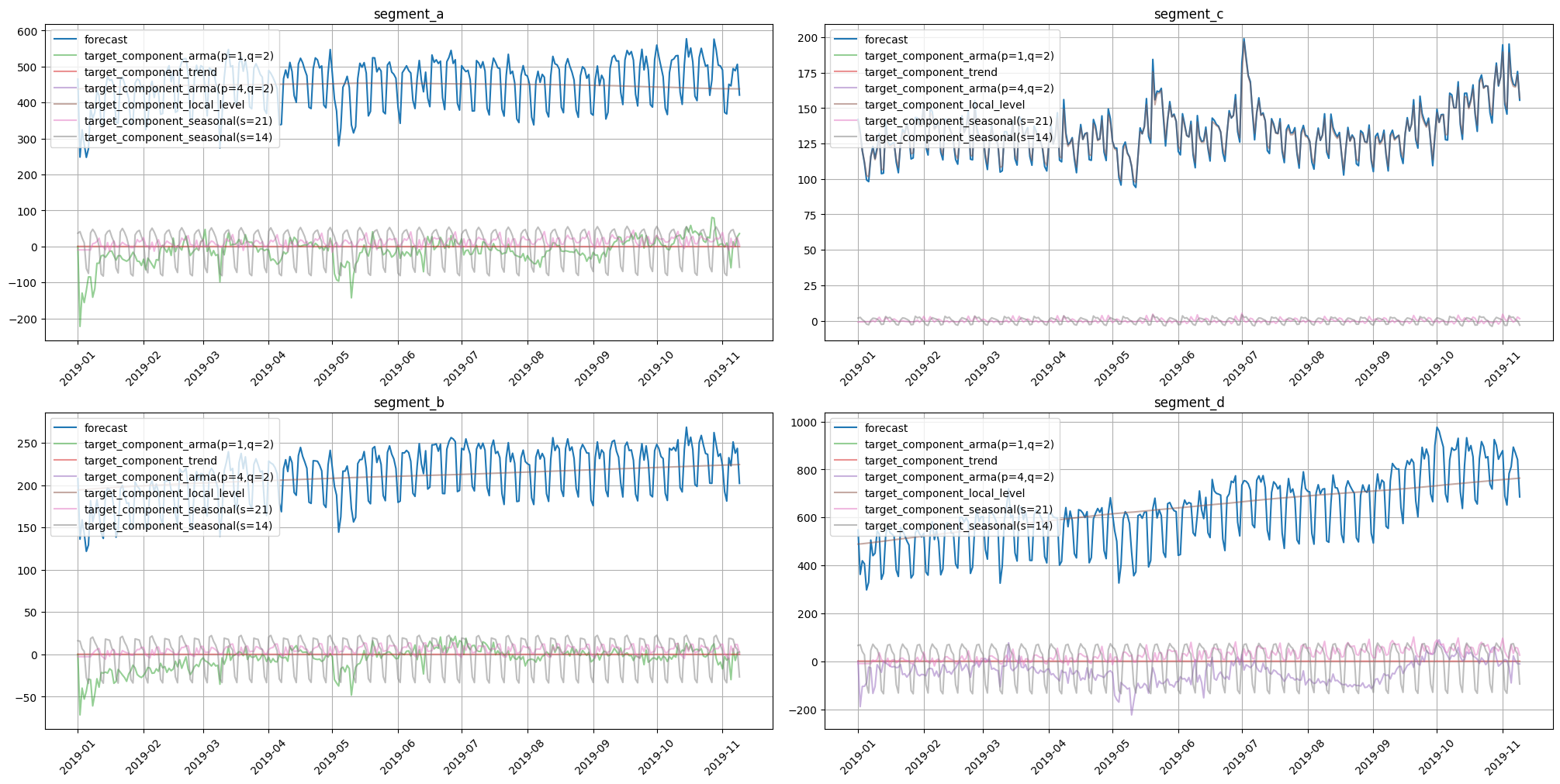
For estimation of out-of-sample forecast decomposition, use forecast with return_components=True.
[25]:
out_of_sample_forecast = model.forecast(ts=future, return_components=True)
plot_forecast_decomposition(forecast_ts=out_of_sample_forecast, mode="joint", columns_num=2, show_grid=True)
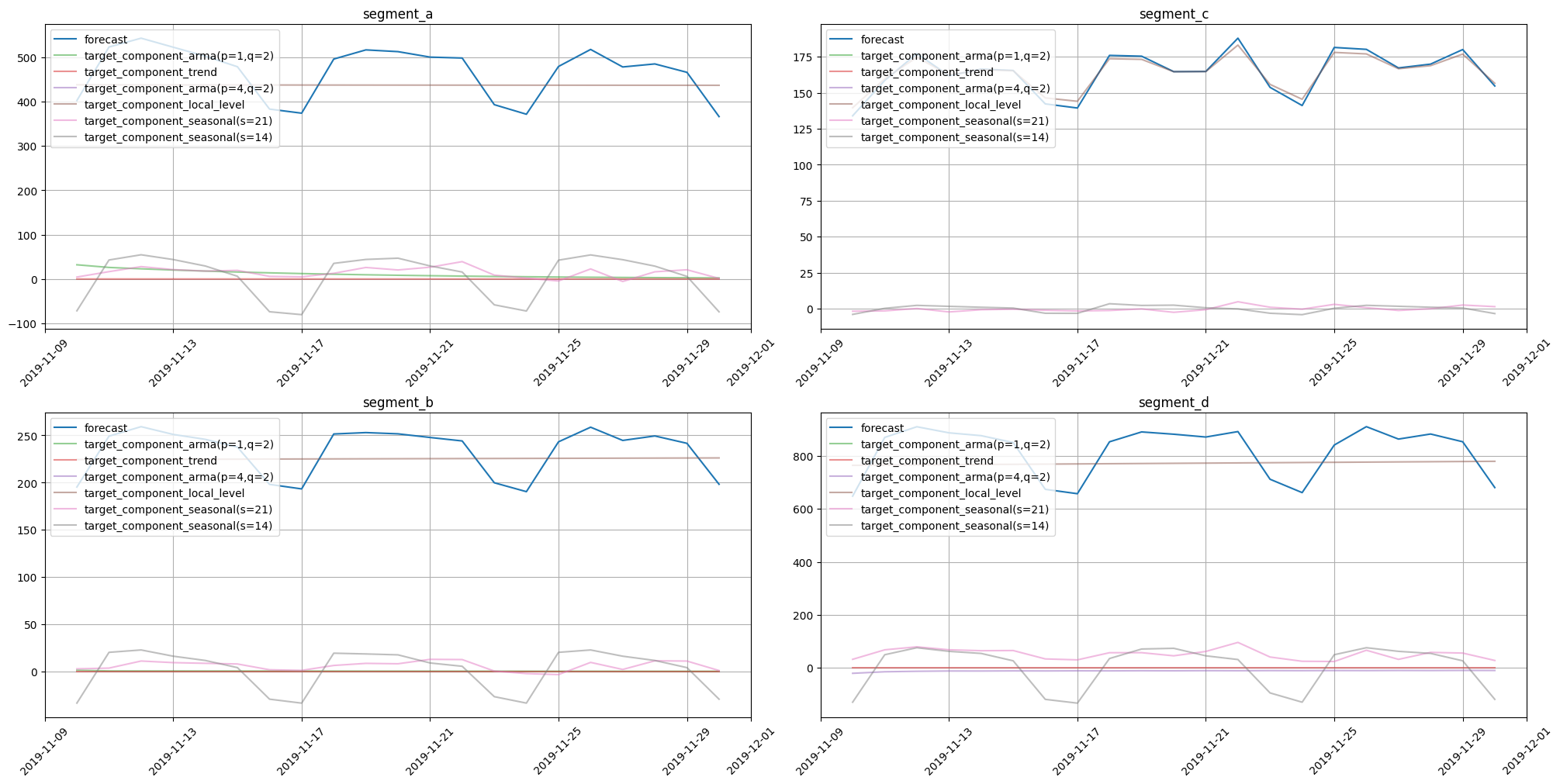
As expected, the decomposition form is the same for in-sample and out-of-sample cases.
3. Accessing target components#
This section shows how one can manipulate forecast components using the TSDataset interface.
Let’s populate our data with lag features and fit the CatBoostPerSegmentModel. We will use this setup to estimate forecast with additive components.
[26]:
ts_with_lags = deepcopy(ts)
ts_with_lags.fit_transform(transforms=transforms)
model = CatBoostPerSegmentModel()
model.fit(ts=ts_with_lags);
Now we can estimate forecasts with forecast decomposition.
[27]:
forecast = model.forecast(ts=ts_with_lags, return_components=True)
forecast
[27]:
| segment | segment_a | ... | segment_d | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| feature | lag_21 | lag_28 | lag_35 | lag_42 | lag_49 | lag_56 | target | target_component_lag_21 | target_component_lag_28 | target_component_lag_35 | ... | lag_42 | lag_49 | lag_56 | target | target_component_lag_21 | target_component_lag_28 | target_component_lag_35 | target_component_lag_42 | target_component_lag_49 | target_component_lag_56 |
| timestamp | |||||||||||||||||||||
| 2019-01-01 | NaN | NaN | NaN | NaN | NaN | NaN | 368.960244 | 52.677657 | 45.848608 | 59.139714 | ... | NaN | NaN | NaN | 440.294693 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| 2019-01-02 | NaN | NaN | NaN | NaN | NaN | NaN | 368.960244 | 52.677657 | 45.848608 | 59.139714 | ... | NaN | NaN | NaN | 440.294693 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| 2019-01-03 | NaN | NaN | NaN | NaN | NaN | NaN | 368.960244 | 52.677657 | 45.848608 | 59.139714 | ... | NaN | NaN | NaN | 440.294693 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| 2019-01-04 | NaN | NaN | NaN | NaN | NaN | NaN | 368.960244 | 52.677657 | 45.848608 | 59.139714 | ... | NaN | NaN | NaN | 440.294693 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| 2019-01-05 | NaN | NaN | NaN | NaN | NaN | NaN | 368.960244 | 52.677657 | 45.848608 | 59.139714 | ... | NaN | NaN | NaN | 440.294693 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2019-11-26 | 510.0 | 502.0 | 532.0 | 582.0 | 528.0 | 558.0 | 587.562771 | 92.622123 | 93.063689 | 102.406833 | ... | 931.0 | 879.0 | 1037.0 | 937.554113 | 186.185095 | 152.507876 | 144.561146 | 142.979337 | 137.269227 | 174.051432 |
| 2019-11-27 | 501.0 | 497.0 | 515.0 | 559.0 | 550.0 | 516.0 | 602.751237 | 93.055945 | 93.196738 | 98.617847 | ... | 897.0 | 886.0 | 969.0 | 941.766157 | 189.933535 | 153.970751 | 143.035390 | 142.433922 | 137.140238 | 175.252321 |
| 2019-11-28 | 525.0 | 501.0 | 520.0 | 543.0 | 547.0 | 489.0 | 556.927263 | 89.108979 | 94.226170 | 90.372332 | ... | 882.0 | 934.0 | 929.0 | 894.837318 | 181.561275 | 154.268641 | 139.273730 | 136.903530 | 130.007170 | 152.822973 |
| 2019-11-29 | 534.0 | 480.0 | 511.0 | 523.0 | 544.0 | 471.0 | 568.569172 | 96.026571 | 92.935954 | 88.949103 | ... | 843.0 | 885.0 | 874.0 | 899.518552 | 178.867363 | 163.091693 | 144.959843 | 132.615508 | 135.207526 | 144.776619 |
| 2019-11-30 | 430.0 | 384.0 | 502.0 | 422.0 | 423.0 | 371.0 | 499.505858 | 81.304877 | 65.772926 | 113.489016 | ... | 652.0 | 672.0 | 664.0 | 720.744048 | 108.165250 | 129.946841 | 111.854389 | 124.573300 | 121.123109 | 125.081158 |
334 rows × 52 columns
Note that we have additional columns prefixed with target_component_. These are individual effects that contributed to the overall forecast.
One can obtain forecast components separately from other forecast data using get_target_components.
[28]:
forecast.get_target_components()
[28]:
| segment | segment_a | segment_b | ... | segment_c | segment_d | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| feature | target_component_lag_21 | target_component_lag_28 | target_component_lag_35 | target_component_lag_42 | target_component_lag_49 | target_component_lag_56 | target_component_lag_21 | target_component_lag_28 | target_component_lag_35 | target_component_lag_42 | ... | target_component_lag_35 | target_component_lag_42 | target_component_lag_49 | target_component_lag_56 | target_component_lag_21 | target_component_lag_28 | target_component_lag_35 | target_component_lag_42 | target_component_lag_49 | target_component_lag_56 |
| timestamp | |||||||||||||||||||||
| 2019-01-01 | 52.677657 | 45.848608 | 59.139714 | 69.745969 | 69.187315 | 72.360981 | 29.190551 | 23.342434 | 27.285093 | 28.338942 | ... | 18.093097 | 13.173772 | 20.646325 | 19.443199 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| 2019-01-02 | 52.677657 | 45.848608 | 59.139714 | 69.745969 | 69.187315 | 72.360981 | 29.190551 | 23.342434 | 27.285093 | 28.338942 | ... | 18.093097 | 13.173772 | 20.646325 | 19.443199 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| 2019-01-03 | 52.677657 | 45.848608 | 59.139714 | 69.745969 | 69.187315 | 72.360981 | 29.190551 | 23.342434 | 27.285093 | 28.338942 | ... | 18.093097 | 13.173772 | 20.646325 | 19.443199 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| 2019-01-04 | 52.677657 | 45.848608 | 59.139714 | 69.745969 | 69.187315 | 72.360981 | 29.190551 | 23.342434 | 27.285093 | 28.338942 | ... | 18.093097 | 13.173772 | 20.646325 | 19.443199 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| 2019-01-05 | 52.677657 | 45.848608 | 59.139714 | 69.745969 | 69.187315 | 72.360981 | 29.190551 | 23.342434 | 27.285093 | 28.338942 | ... | 18.093097 | 13.173772 | 20.646325 | 19.443199 | 58.143024 | 43.773274 | 92.546575 | 76.282320 | 79.442884 | 90.106617 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2019-11-26 | 92.622123 | 93.063689 | 102.406833 | 115.592269 | 74.912398 | 108.965459 | 39.646473 | 41.938191 | 48.057205 | 42.905137 | ... | 28.693191 | 44.746001 | 29.506321 | 24.909083 | 186.185095 | 152.507876 | 144.561146 | 142.979337 | 137.269227 | 174.051432 |
| 2019-11-27 | 93.055945 | 93.196738 | 98.617847 | 104.375155 | 114.013395 | 99.492157 | 44.803978 | 42.526073 | 44.869424 | 44.210031 | ... | 24.689802 | 48.773621 | 28.103322 | 29.071382 | 189.933535 | 153.970751 | 143.035390 | 142.433922 | 137.140238 | 175.252321 |
| 2019-11-28 | 89.108979 | 94.226170 | 90.372332 | 88.756972 | 112.596508 | 81.866302 | 43.636738 | 39.279155 | 41.455011 | 41.251943 | ... | 25.204180 | 49.273745 | 30.080450 | 29.670928 | 181.561275 | 154.268641 | 139.273730 | 136.903530 | 130.007170 | 152.822973 |
| 2019-11-29 | 96.026571 | 92.935954 | 88.949103 | 89.018761 | 117.011601 | 84.627183 | 41.949065 | 38.703364 | 42.617386 | 40.808739 | ... | 22.174713 | 48.547700 | 28.981421 | 26.047110 | 178.867363 | 163.091693 | 144.959843 | 132.615508 | 135.207526 | 144.776619 |
| 2019-11-30 | 81.304877 | 65.772926 | 113.489016 | 86.668521 | 78.966691 | 73.303827 | 38.118666 | 33.999578 | 31.914988 | 33.683397 | ... | 17.088639 | 45.224635 | 22.134809 | 24.102108 | 108.165250 | 129.946841 | 111.854389 | 124.573300 | 121.123109 | 125.081158 |
334 rows × 24 columns
There is a possibility to remove components. It can be achieved using drop_target_components. This function will remove components inplace. We can ensure that our forecast dataset no longer has any components by using the target_components_names property.
[29]:
components = forecast.get_target_components()
forecast.drop_target_components()
forecast.target_components_names
[29]:
()
There is a possibility to attach components to the forecast dataset as well. The main constraint on components is that, being attached, they should sum up to the target at each timestamp.
[30]:
forecast.add_target_components(components)
forecast.target_components_names
[30]:
('target_component_lag_21',
'target_component_lag_28',
'target_component_lag_35',
'target_component_lag_42',
'target_component_lag_49',
'target_component_lag_56')
4. Regressors relevance#
This section shows how regressors relevance could be estimated.
There are two types of relevance estimation in the ETNA library
statistical, based on
tsfresh(StatisticsRelevanceTable)model based (
ModelRelevanceTable)
[31]:
from sklearn.ensemble import RandomForestRegressor
from etna.analysis import ModelRelevanceTable
from etna.analysis import StatisticsRelevanceTable
from etna.analysis import plot_feature_relevance
4.1 Feature relevance#
The first step is to prepare the data. Here, we only need features and estimated forecasts.
[32]:
target_with_features = deepcopy(forecast)
target_with_features.drop_target_components()
Let’s estimate feature relevance using a statistical approach. Results can be shown with the help of the plot_feature_relevance function.
[33]:
plot_feature_relevance(ts=target_with_features, relevance_table=StatisticsRelevanceTable())
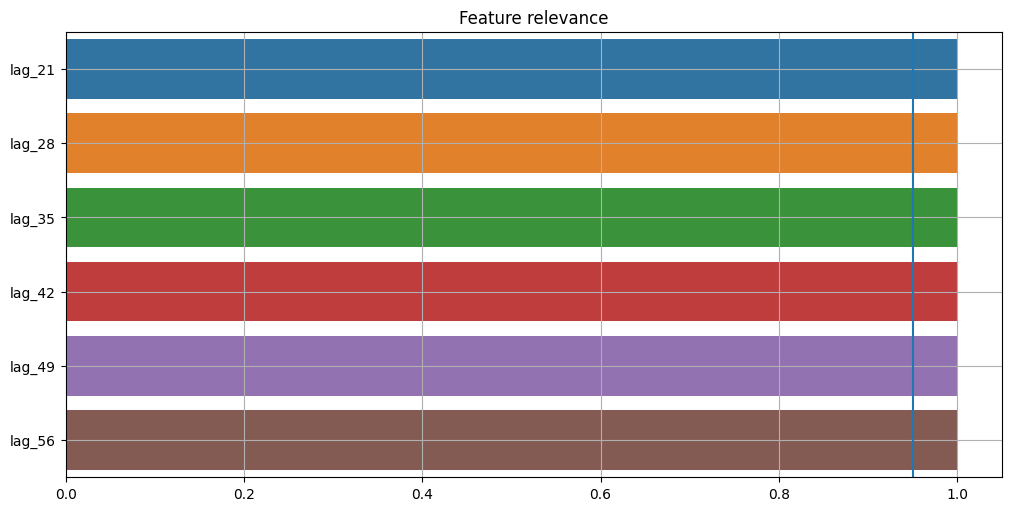
A statistical approach shows that all features have the same relevance. The blue vertical line on the chart represents the significance level. Values that lie to the right of this line have p-value < alpha and values that lie to the left have p-value > alpha. Here we see that all features are significant at the default level of alpha = 0.05. Significance level available only for a statistical approach.
We can use a separate tree-based estimator that is able to provide feature relevance to estimate such values. In this case, we can use RandomForestRegressor.
[34]:
plot_feature_relevance(
ts=target_with_features,
relevance_table=ModelRelevanceTable(),
relevance_params={"model": RandomForestRegressor(random_state=1)},
)
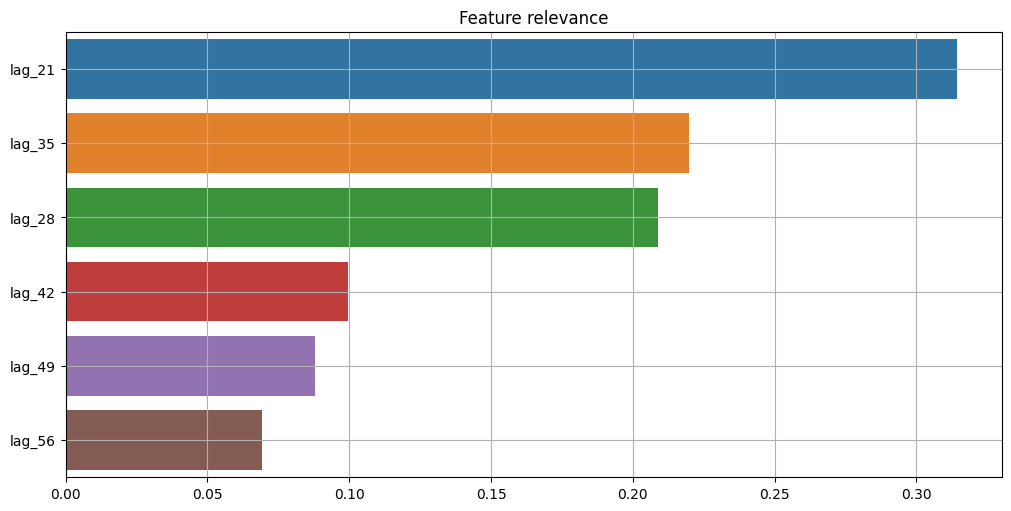
We can see that results from this approach are completely different from statistical results. The main reason is the relevance estimation process. In ModelRelevanceTable, a separate estimator provides feature_importances_, while in StatisticsRelevanceTable statistics from tsfresh are used.
4.2 Components relevance#
We can use the same instruments to estimate relevance for each target component.
First, let’s select only the forecasts with corresponding components from the dataset.
[35]:
target_with_components = TSDataset(df=forecast[:, :, "target"], freq=forecast.freq)
target_components = forecast.get_target_components()
target_with_components.add_target_components(target_components)
Here we can use the same setup with tree-based relevance estimator.
[36]:
plot_feature_relevance(
ts=target_with_components,
relevance_table=ModelRelevanceTable(),
relevance_params={"model": RandomForestRegressor(random_state=1)},
)
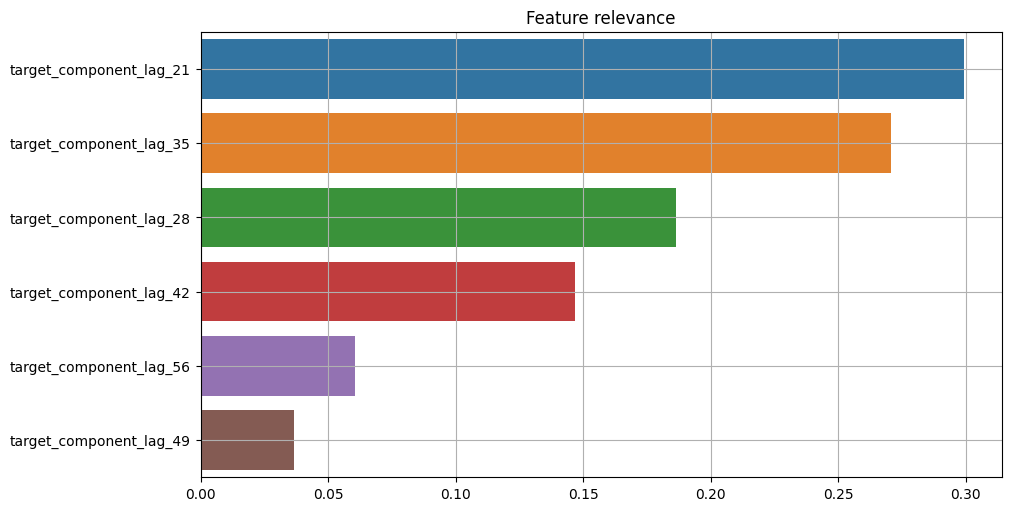
Results show a strong correlation between the relevance of features and the relevance of corresponding components. Note that values are actually different when comparing components to features relevance.
In this notebook we showed how one can decompose in-sample and out-of-sample forecasts in the ETNA library. This decomposition has additive properties and hence may be used for forecast interpretation.
Also, we showed how to estimate regressors relevance with different methods and display the results.